1年 比例反比例の応用 4 問題文 PがAを出発してからx秒後(誤) PがBを出発してからx秒後(正) 2年 連立方程式 解と係数 (1)問題, (3)答b=5(誤) b=3(正)13 解の公式を使った、2次方程式の解き方とは? 14 解の公式の例題連立の計算問題 基礎から標準問題までの練習問題と、例題による解き方の説明 次の2次方程式を解きなさい x 2 9= 0 x 2 16= 0 x 2 3= 0 x 2 11= 0 x 2 75= 0 x 2 98= 0 3x 2 9= 0 2x 2 4= 0二次方程式の解き方(置き換え因数分解)高校数学Ⅰ 二次方程(4) ある学校では全校生徒数は5人で,男子の ,女子の がバス通学をしている. バス通学をしている生徒が全部で150人であるとき,男子の総数を x (人),女子の総数を y (人)として, x , y が満たす連立方程式を求めなさい. HELP 全校生徒数は5人だから, xy=5
從推導一元二次方程的公式解看個性 線代啟示錄
連立 方程式 公式
連立 方程式 公式-未知数が2個の連立1次方程式の場合 axby=p cxdy=q すなわち の解は( ad−bc≠0 のとき) となる. 未知数が3個の連立1次方程式の場合 axbycz=p dxeyfz=q gxhyiz=r すなわち の解をクラメールの公式を使って書くと(分母が0でないとき)連立方程式 2元1次方程式とは 2xy=8 のように 2つの文字を含む1次方程式が 2元1次方程式 で、 2元1次方程式を成り立たせる文字の値の組を 解 という。 2元1次方程式の解は無数にある。 例 2xy=8 の解は x=1,y=6 やx=2,y=4など


連立方程式を解く 規則集4 中学から数学だいすき
13 解の公式を使った、2次方程式の解き方とは? 14 解の公式の例題連立の計算問題 基礎から標準問題までの練習問題と、例題による解き方の説明 次の2次方程式を解きなさい x 2 9= 0 x 2 16= 0 x 2 3= 0 x 2 11= 0 x 2 75= 0 x 2 98= 0 3x 2 9= 0 2x 2 4= 0二次方程式の解き方(置き換え因数分解)高校数学Ⅰ 二次方程2年 連立方程式 解と係数 (1)問題, (3)答b=5(誤) b=3(正) 1年 文字式の計算2(加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5(3)解答(0,4)→(0,4)または(0,4) 1年 文字式の計算3(乗除) 答3③9c誤→49c正2つの式から連立方程式を作ると $$\begin{eqnarray} \left\{ \begin{array}{l} 15x 15y = 3600 \\ 30x – 30y = 3600 \end{array} \right \end{eqnarray}$$ あとは、この方程式を解いていくだけです。 係数を揃えて、加減法で解いていきます。 $$30x30y=70$$ $$30x30y=3600$$ それぞれの式を足すと
当ページでは連立1次方程式を、クラメルの公式を用いて、解く方法をご紹介いたします。 掃き出し法を使って連立一次方程式を解く方法に関してはこちらで紹介しております。 クラメルの公式 公式 \(\begin{eqnarray} \left\{ \begin{array}{l} a_{11}x_1 a_{12}x_2連立 次方程式 は、数値計算 を試みる人の前に頻繁に立ち現れる問題です。 方程式は = = で表記されます。未知数は = 個の です。 を行列形式で書けば = です。連立 次方程式の数値解法 とは、行列 とベクト ル に対し、 をみたす を数値的に求める方法 です。1 クラメールの公式 A が正則(det A ≠0)でA1 が存在する)の時 x = A1b A A x j j = (j = 1, 2, , n) |A j| A でその第j 列とb とを交換して得られる行列A j の行列式 解法例:以下の二元連立一次方程式をクラメールの公式を使って解く。 2 2 5 8 3 4 10 1 2 1 = = x x x x
連立方程式の解き方 連立方程式を解くには、主に2つの方法があります。 まず、 代入法 と呼ばれる方法です。 片方の式をx= や y= の形に変えて、それをもう片方の式に代入することで文字を1つ減らし、答えをもとめる方法です。2年 連立方程式 解と係数 (1)問題, (3)答b=5(誤) b=3(正) 1年 文字式の計算2(加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5(3)解答(0,4)→(0,4)または(0,4) 1年 文字式の計算3(乗除) 答3③9c誤→49c正A = a 1 b 1 a 2 b 2 ≠ 0 のとき,連立方程式の解は, x = 1 A c 1 b 1 c 2 b 2 = c 1 b 1 c 2 b 2 a 1 b 1 a 2 b 2 y = 1 A a 1 c 1 a 2 c 2 = a 1 c 1 a 2 c 2 a 1 b 1 a 2 b 2 で与えられる. これらの解を表す式を クラメルの公式 という. 3元1次連立方程式の場合


測評網 國一下 數學第一次段考 複習錦囊



3 3克拉瑪公式
連立1 次方程式の解法として、線形代数の教科書にはクラーメル(Cramer) の公式や掃き出し 法(Jordan の消去法ともいう) が説明されていることが多いが、ガウスの消去法は、掃き出し法を 改良したものである。 例として次の方程式を取りあげて説明しよう。 (2連立方程式(れんりつほうていしき)とは、2つ以上の方程式の組です。複数の方程式に対して、複数の未知数があります。 上記の連立方程式のx、yの解は、それぞれ共通した値です。 2次方程式の解の公式とは?1分でわかる意味、覚え方、公式の導出



Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



南一x 均一 數學會考特訓班講義 一到六冊 Shareclass



Word10 数学公式 联立方程 大括号内方程组如何左对齐 Ai Algorithms 博客园


Ch6 聯立方程式 陳權數學免費影音教室



二次方程式 維基百科 自由的百科全書



隨筆誌 二下2 3三元一次聯立方程式 克拉瑪法則證明



偉智數學wisemath 生活數學 試誤法 近日 偉智數學wise Math Facebook



數學1到4冊 Xmind Mind Mapping Software



國中數學公式寶典by Chidopi Co Ltd Taiwan


Excel函數案例之 使用excel求解一元二次方程 愛經驗
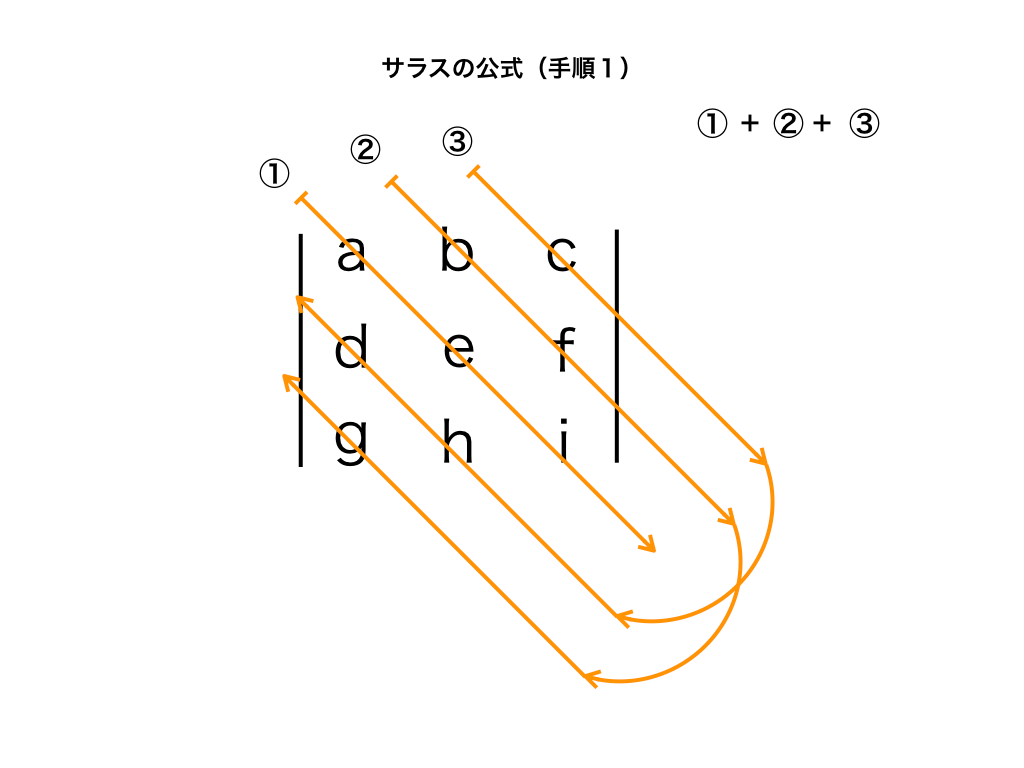


掃き出し法で連立方程式を解く手順とコツを解説


測評網 國一下 數學第一次段考 複習錦囊


連立方程式を解く 規則集4 中学から数学だいすき


クラメルの公式を使った問題です なぜ 連立方程式から矢印のように表 Yahoo 知恵袋


第1章 連立方程式



数学领域 数学课程纲要下载 在线阅读 爱问共享资料



一個三角函數求值公式及其應用 每日頭條
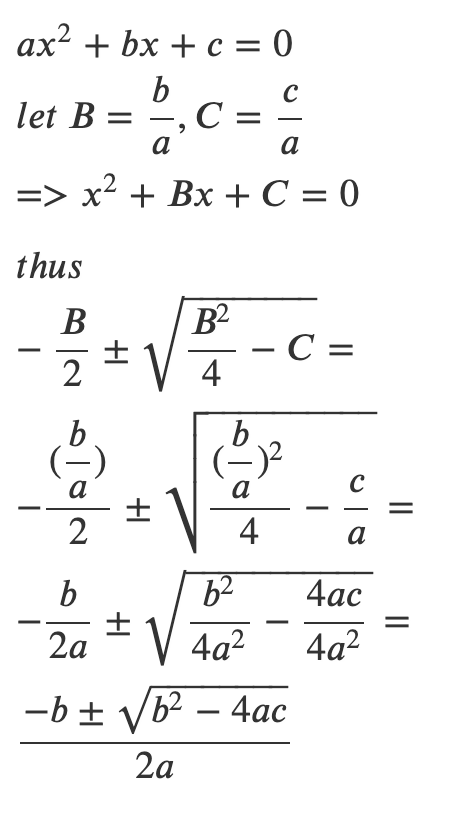


這幾天又有一篇很紅的數學文章 被大家轉發來轉發去的 By Summit Suen Medium
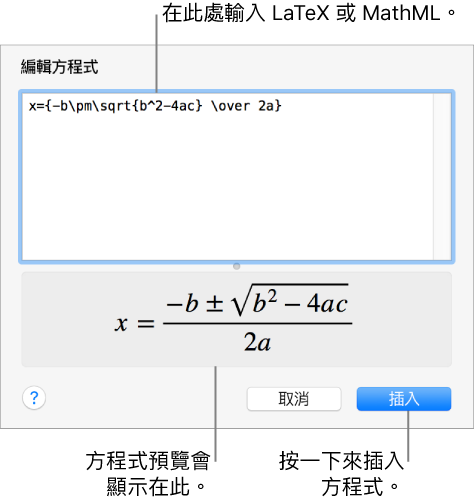


Mac 版pages 在pages 中加入數學方程式



數學總複習



翻轉學習影片 高中 數學 三元一次聯立方程組 練習10


數學女孩秘密筆記 公式 圖形篇 蝦皮購物



三元一次聯立方程式 克拉瑪公式說明 Youtube



小数の連立方程式の解き方 両辺を10倍や100倍しよう 中学や高校の数学の計算問題



心に強く訴える連立3 元1 次方程式 壁紙配布



一元二次方程式的公式解及二次函数图形 百度文库


名師課輔網 數學學測是否有某些單元不用考



二次方程式 維基百科 自由的百科全書



連立方程式公式



高中數學三元一次方程組的克拉瑪公式 Youtube



一個三角函數求值公式及其應用 每日頭條



トップ100連立方程式例題 ただぬりえ



Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download


1元1次方程 2元一次方程 一元十次方程 一元整式方程


以下の連立方程式をクラメルの公式で解きたいのですが 右辺が整数と Yahoo 知恵袋



用google Docs 寫數學公式 就像word 插入方程式



加減法 連立方程式の解き方 中学数学 By じょばんに マナペディア



隨筆誌 一下1 2解二元一次聯立方程式 指數問題


從推導一元二次方程的公式解看個性 線代啟示錄


第1章 連立方程式



聯立方程式 Labview Labview360論壇



陳擎文教學網 Python求解數學式 高中數學 大學數學 工程數學數學 微積分


測評網 國一下 數學第一次段考 複習錦囊



Digital Teaching Materials Of Kosen Fundamental Mathematics For Bilingual Engineering Education Semantic Scholar



指考甲公式



國一下的二元一次連立方程式的變換題型 第一張為題目 第二張為解答 Clear



怎麼知道的 紅線 Clear


Yll討論網 一個線上學習的數學網站 數學討論區 數學論壇含數學遊戲 觀看文章 問題 數學 二元一次聯立方程式



高職暑期銜接課程 國中代數 學思達講義 Shareclass
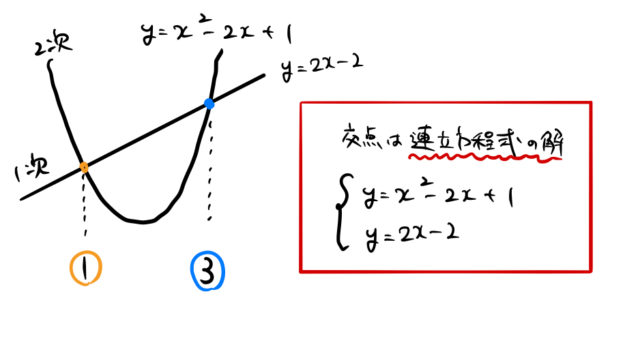


高校数学 面積を求める 1 6公式 1 12公式 1 30公式などパターンまとめ ばたぱら


如何用c 語言解二元一次方程式 C C 語言 伊莉討論區



クラメルの公式による連立1次方程式の解法



高職暑期銜接課程 國中代數 學思達講義 Shareclass



Ppt 第一章乘法公式與多項式powerpoint Presentation Free Download Id


三元一次方程式求連比 紀算 補習班 數學補習班 三重 文理補習班 數學公式 數學題庫 數學競賽 國小數學 國中數學 痞客邦


演算法筆記 Root Finding


從推導一元二次方程的公式解看個性 線代啟示錄



分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題



3 3克拉瑪公式



一元二次方程式的公式解及二次函数图形 百度文库
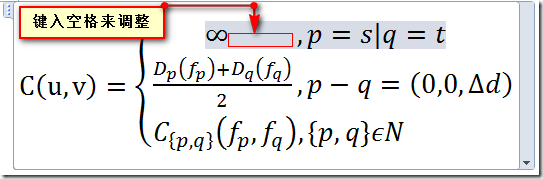


Word10 数学公式 联立方程 大括号内方程组如何左对齐 Ai Algorithms 博客园


連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点



數學心智圖



對稱型二元一次聯立方程式公式解 魔術方塊and數學 隨意窩xuite日誌



东京大学工学系研究科数学套路总结系列 常微分方程式过去问应用型 Kaye Tokyouni的博客 Csdn博客



深度學習的數學基礎 梯度下降法的含義與公式 Codingnote Cc



書記が数学やるだけ 44 逆行列を求める 2 余因子行列 行列のランク 連立方程式 3 クラメールの公式 鈴華書記 Note



柯西色散公式 柯西色散公式指的是法國數學家柯西發現媒質的折射率與真空 華人百科



打遍天下 一元二次方程式 的無敵手 克拉瑪公式 Ishewh的創作 巴哈姆特



Mathtype中的聯立條件是怎樣輸入的 壹讀



國中數學公式寶典by Chidopi Co Ltd Taiwan



Java解四元一次方程 a的博客 Csdn博客



一元二次方程式的公式解及二次函数图形 百度文库



電気磁気工学を学ぶ クラメルの公式


第1章 連立方程式



最新 三連立方程式 Hd壁紙画像fhd



方程解的公式 公式法解方程 解方程 公式法



超越方程式放射公式



Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



大人的數學教室 透過114項定律奠立數學基礎 三民網路書店



高中數學二元一次方程組與克拉瑪公式a Youtube


1 1 1 乘法公式 基礎篇 On Vimeo


大人的數學教室 透過114項定律奠立數學基礎涌井良幸台灣東販 摘要书评试读 京东图书



兩條線的交叉點怎麼算 有什麼公式嗎 Mobile01


克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌



解き方 連立方程式の加減法がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿